And a Case of Dialectics Disowned?

Nonstandard Analysis: A Revolution Under Way?

MARTIN DAVIS
Courant Institute
New York University

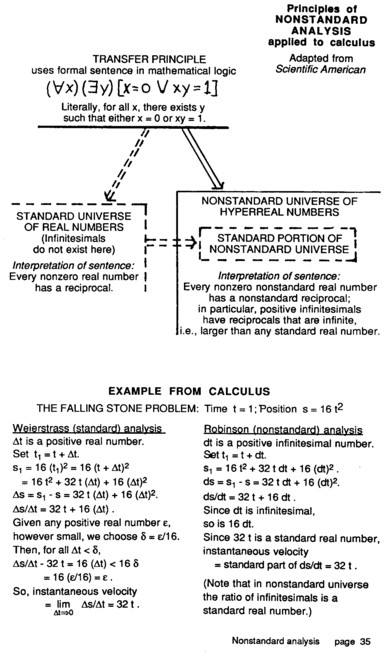
AN INTERVIEW WITH LESTER TALKINGTON. The subject matter of this interview is a paper, "Nonstandard Analysis," by Martin Davis and Reuben Hersh (University of New Mexico) that appeared in Scientific American June 1972. It deals with a new system of analysis created by the late Abraham Robinson, a logician at University of Toronto. Some main features of this system are summed up in a diagram and table on the facing page.

Q. After reading the paper that you wrote with Hersh I made a note to myself saying: "This entire discussion is in a delightful dialectical style." Were you conscious of using dialectical thinking?

A. I have certainly read Marx and Engels, and wouldn't be surprised if Reuben has too. I suppose it's bound to have had some influence. But if you ask what I think about all that now you will get a pretty negative reaction.

Q. Well, I'm concerned here strictly with philosophy of science.

A. That's what I mean. Some things Engels wrote on mathematics in Anti‑Dühring are pretty terrible.

Q. Maybe we could come back to this later. It seems to me that making the infinitesimal once again respectable is a good example of development in which calculus history goes in an upward spiral and back to where it was, though at a higher level.

A. You can certainly put it in that scheme quite happily.

Q. But you haven't thought of it that way?

A. I don't see any special advantage to thinking of it that way but, sure, one certainly understands the idea of an infinitesimal now in a way that was hardly possible in the earlier centuries—and then in the 19th century the whole idea of the infinitesimal was negated, as you might put it in your scheme.

Q. So now we have a negation of the negation. Not long ago I was told sternly not to think of a derivative as a ratio of infinitesimals. Now I am told that I can. Isn't this a revolution?

A. Yes, or think of it as differing from such a ratio by an infinitesimal.

Q. As I understand it, in the hyperreal number system you can manipulate infinitesimals arithmetically or even algebraically.

A. Absolutely. What was really so clever of Robinson was to see how the ideas of model theory in mathematical logic could give you an extension of the number system to include infinitesimals and yet all the usual formal manipulative rules remain true. Not only algebraic. You can do trigonometry, anything you want, just as in dealing with ordinary numbers.

Q. You have the basis for manipulation at both ends of the scale?

A. Right. Abraham Robinson showed how you could embed the ordinary real number system in a larger structure, the hyperreal number system with infinite real numbers as well as infinitesimals. When you are working within the hyperreal system you don't even have to know you're there. In fact, you can't recognize infinitesimals or infinite numbers as such. The means for characterizing them are not present, which is what makes it possible to carry out all the ordinary manipulations. The trick is in moving in and out of the hyperreal universe. You can step outside and then say, "Oh, yes, those were infinitesimals I was working with. In this subject people distinguish between internal and external concepts. The infinitesimal is an external concept. As long as you're in the nonstandard universe, you can't distinguish an infinitesimal from other hyperreal numbers, but outside you can.

Q. Is this an example of different levels of manipulation?

A. I wouldn't put it that way. The two structures, I would say, are at complete equality with one another. You move back and forth from one to the other by means of something called the transfer principle. This principle says of any statement that can be written in a suitable formal language of symbolic logic, if it is true in one structure, it is also true in the other. If you want to be fanciful about it, imagine beings that inhabit the nonstandard universe who can talk to beings in the standard universe by telephone only if they use this particular language. And there's no way of saying in that language what an infinitesimal is. If an inhabitant of the standard universe should say, "I think you live in a nonstandard world because you've got infinitesimals there," the response would be, "I don't see any infinitesimals here. What's an infinitesimal?"

Q. I have wondered if the infinitesimal isn't some sort of primitive, something that in the end you just have to accept rather than try to justify its existence logically.

A. But Robinson did justify its existence logically. That's exactly the nature of his achievement, to show that there is a systematic procedure by which you can replace argumentation that uses infinitesimals with argumentation that doesn't, getting your proof either way.

Q. How much has nonstandard analysis been used? How widely is it accepted in the mathematical world?

A. Not very widely. There are only a handful of enthusiasts, including an important school of nonstandard analysis in Strasbourg, France. But most traditional analysts tend not to have even learned it. Certainly it has not become a mainstream subject. There's basically the problem of articulation with mainstream mathematics. The students have to move up into advanced calculus that's taught the usual way, because that's how the system is set up.

Q. In the paper you state that "in a real sense we already knew what instantaneous velocity was before we learned [the Weierstrass] definition; for the sake of logical consistency we accept a definition that is much harder to understand than the concept being defined." Doesn't this imply that in the end mathematicians and physicists must surely come to accept the new Robinson definition because it is simpler and easier to understand?

A. I think so myself. But that's for history to determine.

Q. Is the resistance purely inertial, or is there also some ideological hostility involved?

A. It's complicated. I haven't found anybody who thinks that nonstandard analysis is wrong or invalid. Any hostility stems from a feeling that it's not going to help with our problems. You can say: "Look what Robinson and Bernstein did with the invariant subspace problem." And they say: "Well, Robinson is a very smart man. If he'd looked at the invariant subspace problem without nonstandard analysis, he probably would have solved it anyway." How can you answer that? He certainly was a very smart man. As I say, history will tell—when young people come along who don't have this big investment from having learned analysis in the usual way.

There's a very interesting man at Princeton named Ed Nelson—everybody agrees he's a topflight mathematician—who is absolutely sold on nonstandard analysis. In fact, the Strasbourg school is very much the result of his influence. He has some definite philosophical concerns that you might find interesting. He's what I would call an ultra-positivist, refusing to make any kind of existential statements. Now there are a good many mathematicians who would philosophically rather not think of infinitesimals as something really existing but simply as concepts they can use and get valid results. For Nelson, however, it's not just the infinitesimals that do not exist; even real numbers do not exist for him. In one of his talks he said that physicists have long since given up on objective reality and only mathematicians continue to cling to it. So his way of expressing nonstandard analysis is ultra-formalistic; there's nothing to it but just a new way of manipulating symbols.

Q. He solves the problem of two worlds by making them both nonexistent?

A. Right. But whether anyone can do the deep things Nelson does without at some level thinking existentially is another question. Afterwards you can always write up the results of the research in a purely formal way.

Q. That seems to me an important distinction. In other words, you think that the discovery of new things in mathematics has to have a materialist basis?

A. Yes, I think that's right. Archimedes left us a wonderful example. He anticipated the differential and integral calculus by solving problems that involved calculating areas for regions bounded by complicated curves such as parabolas. The way he first computed the areas was by the use of physics. For a parabolic segment, he imagined a thin body having this shape and computed the center of gravity using levers.

Q. He used levers literally or figuratively?

A. Figuratively. But then, after solving the problem as one of mechanics, he was enough imbued with Greek rigor to not regard this as a legitimate proof. So he proved it all over again by what he called the method of exhaustion which, in modern terms, is basically integration. For a long time there was a mystery because only the proofs by exhaustion were known. It's easy enough to see how these proofs worked if you already know the answer, but we had no clues as to where the answer had come from. Then somebody found the manuscript by Archimedes titled "Method" in which he told how he got the answers.

Modern mathematicians could learn from this example. There are some lecturers who will produce a beautiful rigorous exposition without a hint as to where the ideas come from, nothing about the usual rough and tumble of developing new ideas, some of which are not so precise, and all of which have been worked over in complicated and amorphous ways. The normal proof comes only at the end.

Q. I think that's often true in physics, too. Getting down to historical origins is important for understanding a mathematical or physical law.

A. It certainly adds a dimension. But it's partly a matter of taste. Some people find that going back to the origin of an idea helps them see it in a useful way. Others find that a distraction because connections are known now that weren't seen then, and things that once required complex and cumbersome calculations can now be done on a more conceptual basis. Some mathematicians work comfortably in a historical framework; others don't.

Q. Are there limits to Robinson's approach? I'm thinking about the requirement of formal logic in going back and forth between the standard and nonstandard discourse.

A. If you like, the transfer principle is a limit but it also gives the method its power. Without this limit, nonstandard analysis would be trivial, you would not be able to play upon the interrelations of the two systems. But using the principle skillfully is a new craft in itself. You learn what you can and cannot express in this formal language. You have to be tricky. Since you can't express infinitesimals directly, you sometimes have to replace a sentence with a weaker one which can be expressed in the language. Then, after the transfer, you find you can do something at the other side which win get you back what you want. That's the kind of manipulation that practitioners of the art learn to do.

Q. Do you need a new transfer sentence in mathematical logic for each new problem? Say, for each time you formulate a problem in calculus?

A. Not at all. Once you have established the transfer principle you are free to work algebraically in any way you choose within the nonstandard universe. For instance, to take an example from high school algebra, you can solve simultaneous equations or quadratic equations involving infinitesimals. Of course, if your problem involves some mathematical principle for which no transfer sentence exists, then you turn to the art of using this language.

One of the persistently amazing things about mathematics is the power of a formalism. It shows up in Robinson's contribution too. Formalisms always have a greater range of validity than the conditions under which they were derived. Somehow, by the time a truth has been written down in symbolic form, it has captured more than the conditions that produced it. This remarkable power is something that physicists can use freely; they can let themselves go, and not have to worry so much about the consequences as mathematicians do, because there's always the bedrock of experiment at the other end for a check on their work. We mathematicians don't have that check so we have to be a little more cautious.

Q. In your paper, for an example of "infinitesimal reasoning," you quote L'Hôpital's axiom that "two quantities differing by an infinitesimal can be considered equal," which means, as you point out, “the quantities are at the same time considered to be equal to each other and not equal to each other!” Doesn't this dialectical contradiction still hold in the standard world even though it has been resolved in the nonstandard world?

A. No, in the standard world there is only one infinitesimal and that has the value zero, so the symbols have only a formal meaning as the limit of a quotient. So you go over to the nonstandard world for a quotient of infinitesimals.

Q. You deal so fluently with concepts such as dialectical contradictions that I am puzzled. Why is it that I recognized the application of dialectical materialist principles in your paper with Hersh yet you do not feel they are any kind of guide in your conscious work?

A. The way I'd put it is that the so‑called laws of dialectics are schemes or patterns that apply to all kinds of discourse. But I don't think they are particularly useful as a guide to making discoveries, and they're certainly not a useful guide in establishing their validity. You can talk about transforming quantity into quality from now to the end of time, but the real problem is to understand what happens in the process you're describing, what's happening in, say, the laws for a physical change of phase. I don't think dialectics is the least help for that.

Q. Engels, and many since, have said that you have to understand the science, the particular discipline itself, in order to think about it, dialectically or otherwise. Our journal is devoted to showing how materialist dialectics help, especially in the discovery process. Isn't it possible that in your creative work you may be using some of the ideas of Marx and Engels even unconsciously?

A. Who knows what I do unconsciously! It's certainly true that everything keeps changing and that the way things change is that they cease to have certain properties so that, when you're looking at that particular property, you see a contradiction. You say: "Look, what was this way has become that way." In Hegel's idealist view, things did not exist, they only had properties, so that seeing change as the alteration of properties was very natural. In that sense, everybody thinks dialectically. But this is not the use of laws in the same way as using the law of gravitation to predict an eclipse or the laws of logic to carry out a deduction. I see dialectics rather as a scheme that can be applied after the fact. And anybody can use such a scheme. If the Moonies wanted to use dialectics, they could write all their doctrines in dialectical terms.

Q. But not in dialectical materialist terms.

A. That's true.

Q. Dialectics by itself has no content. It's like mathematics.

A. I grant the point. But the union of the materialist outlook with the so-called dialectical laws can still be applied to any material system of things.

Q. That's what both Engels and Lenin said, that scientists in their work become spontaneous dialectical materialists, without knowing it. That's because these principles do reflect the processes of change in nature.

A. As far as I can see, the laws do not say anything more than that we live in a changing world. I don't see how they can help us look for the underlying laws that govern these changes, which is what's important.

Q. Lots of Marxists think they do in the social realm. Dialectical materialism was invented by Marx and Engels while they were studying the process of material change in society, and this philosophy has helped to further the process of social change. By the way, what were the absurd things you found in Anti‑Dühring?

A. Engels was about 100 years behind the times on mathematics. For example, he said preposterous things about imaginary numbers. As far as he was concerned they existed as outright contradictions in mathematics itself.

Q. But didn't he joke about this later, referring to the "unrecognized genius of a mathematician" who complained in a letter to Marx about Engels' “wanton attack on the honour of √‑l”? That was in the second edition of Anti‑Dühring.

A. Engels' "joke" about √‑l is really not very funny. The "genius of a mathematician" evidently took the trouble to point out that, given the fact that "every negative magnitude multiplied by itself gives a positive square," this does not imply that "It is a contradiction that a negative magnitude should be the square of anything . . ." [Anti‑Dühring]. It merely implies that a negative number cannot be the square of another negative quantity, so that √‑l can be neither positive nor negative (nor zero). But this is no more a contradiction than is the fact that many Americans are neither Democrats nor Republicans.

Q. Let's face reality. Neither Marx nor Engels (nor Lenin) was a mathematician or a natural scientist. They left a lot for us to do in these areas. Our journal is trying to do something about this. We want to show how the Marxist world view can really help scientists deal with the philosophical problems of their professional work. Give us a chance.

A. I don't question that any rational statement about the world, changing as it is, will fit into a dialectical scheme as well as a materialist one. But the critical question is whether anything is gained by consciously fitting things into a scheme of dialectics.

Q. I think most Marxists would agree with you that conscious retrofitting is not the answer. That's what Lenin called "empty dialectics" [Notebooks p 280]. But didn't you just agree that you yourself may be using dialectics unconsciously? Now how do you know that your conscious awareness of dialectics is not contributing unconsciously to your mathematical creativity?

A. You are right. By the very definition of "unconscious" I cannot claim to know (consciously) that I am not making unconscious use of dialectics or, for that matter, of the doctrine of transubstantiation. Again I want to say that Engels' errors and his "joke" about √‑l are not very funny.

At this point, both parties agreed to let the matter rest. For those interested in learning more about nonstandard analysis, Prof. Davis recommends Jerome Keisler's "Elementary Calculus" (Boston: Prindle, Weber & Schmidt 1976).

ADDENDA. (1) The troubled state of calculus was the subject of a recent special meeting of concerned educators at Tulane. Participants agreed that current curricula and teaching methods are a drag on both faculty and students (and, thereby, on the science and engineering professions), and that change is made difficult by entrenched textbook interests. However, judging from a two‑page report in Science News (5 Apr 1986) and five letters from teachers and students (7 June), the possibility of simplifying the concepts of calculus by the conceptual approach of nonstandard analysis was not mentioned at the meeting.

(2) On rereading the interview it seems significant that Prof. Davis consistently referred to "dialectical laws," as in a formal context, while I referred to "dialectical principles," a concept more in keeping with the view of dialectical logic as inherently informal [cf. S&N #4: 77f, #5: 3‑5]. [L.T.]

Nonstandard Analysis      Page 35	An "abacist" (right) competes against an "algorist" in a 16th‑century print Nonstandard Analysis      Page 39

SOURCE: Davis, Martin. “Nonstandard Analysis: A Revolution Under Way?”, interview with Lester Talkington, Science and Nature, Nos. 7/8 (1986), pp. 34-42.

Note: Dirk Struik's remarks immediately follow article (p. 42).

On Engels and the Dialectics of Calculus

We can now understand Engels' remark that the variable quantity introduced motion into mathematics, and with it dialectics and hence the calculus. This should not, however, be understood in the sense that mathematics before Descartes was undialectical. Engels himself observed that even the simplest mathematical relations show primitive dialectical structure. Indeed, multiplication originated as an abbreviated addition, division as an abbreviated subtraction, and we learn to consider a subtraction as an addition, a division as a multiplication [Dialectics of Nature 1940, pp 198f]. This last is already a clear case of a development in opposites, hence of a dialectical development, and it is certainly not a little game in which we amuse ourselves by calling John Peter, and Peter John. It is a mighty movement from the primitive to the complicated, from the simple to the difficult, from positive to negative, from integer to fraction, from rational to irrational, from real to imaginary, from the simple abstract images of real relations to the profound abstractions of modern mathematics, which yet are images of objective relations.

What Engels meant by his remark is that dialectics entered into mathematics in full force, in a formulation which does not use the more primitive dialectics of formal logic. Indeed, the foundations of the calculus, with its infinitesimals, will always remain a field where the laws of dialectics can be studied in great detail, so that even the most minute elements can be seen in a dear light No wonder that it has been a favorite field for dialectical philosophers, such as Leibniz, Hegel and Marx.

— DIRK STRUIK, " Concerning Mathematics." Science and Society vol 1, pp 86f.

It is of course clear that a mathematician, facing a problem, is not going to say, "Now I have to use dialectical materialism." He will get better results if he says, for example, "Now I have to use Lebesgue integration," or, "Now I have to get myself a drink.'' Philosophy does not replace scientific technique; it can, however, do much to clarify it. Personally, I always keep a dialectical kind of materialist approach in the back of my mind, whether I think of the difficulties of Cory Aquino's presidency, the relation of Marx to Thoreau, or the transformation of mathematics in the days from Euclid to Newton.

Engels was not "100 years behind" even if he slipped up on i = √‑l. Engels made more such blunders in his life, and we can learn even from those. The general position on math in Anti‑Dühring is sound, as Aleksandrov correctly claims. * As for that i = √‑l business, when you consider the position of both Marx and Engels on math in the 1870s, don't forget that they were in England; except in algebra and geometry, England was far behind the Continent. They had no opportunity to talk to leading mathematicians, only to Engels' friend Samuel Moore who was just an intelligent layman. And there were enough authorities in England (such as the astronomer Airy, 1801‑1892), who found i = √‑l so fantastic that they would not touch it ("pure imagination").

Do not ask me what I think of nonstandard analysis. I have not yet studied it. But, for me, it shows that, since Robinson et al. have every right to philosophize today about the foundations of the calculus, we cannot blame old Marx for worrying about them in the 1870s.

— DIRK STRUIK, personal communication 1986.

* A. D. Aleksandrov, "Mathematics: Its Essential Nature and Laws of Development." Science and Nature No. 3 pp 22‑42.

Science and Nature, Table of Contents, issues #1-10 (1978-1989)

Alienation in American Society (Selections)
by Fritz Pappenheim, with Dirk Struik

Marx and Marxism Web Guide

Vienna Circle, Karl Popper, Frankfurt School, Marxism, McCarthyism & American Philosophy: Selected Bibliography

Offsite:

Marx's Mathematical Manuscripts

“Friedrich Engels and Mathematics” by Jean van Heijenoort

CONTACT Ralph Dumain