INCLOSURE SCHEMA

As we have seen . . . all the paradoxes of self‑reference (including Berkeley's Paradox and the Fifth Antinomy) are inclosure contradictions; that is, they all instantiate the Inclosure Schema, which, to remind the reader, concerns properties φ and ψ, and a function δ such that:

(1) Ω = {y; φ(y)} exists and ψ(Ω)                   Existence

(2) if x ⊂ Ω and ψ(x)      (a) δ(x) not-∈   x    Transcendence

                                       (b) δ(x) ∈ Ω           Closure

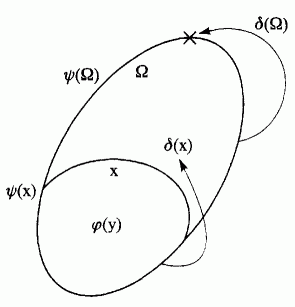
One might depict these conditions as in Figure 1. The large oval is Ω, the set of all φ things. x is any subset of Ω satisfying ψ, and δ applied to this takes us out of x but into Ω. Applying δ to Ω takes us both into and out of Ω. This is somewhat difficult to depict(!). I have done so by taking δ(Ω) to be a spot on the boundary of Ω. [1]

1 There is something rather appropriate about this. The boundary is, in its own way, paradoxical, both joining and separating the inside and the outside.

Source: Priest, Graham. Beyond the Limits of Thought, 2nd ed. (Oxford: Clarendon Press; New York: Oxford University Press, 2002), p. 156.

Note: I can't find a readable symbol for the following, so:

not-∈ = not an element of

Graham Priest, Paraconsistent Logic, and Philosophy, Or, Logic and Reality
by R. Dumain

Graham Priest vs Erwin Marquit on Contradiction by R. Dumain

“What is the Relationship Between Logic and Reality?” by R. Dumain

Philosophy of Paraconsistency & Associated Logics (Web Guide)