 [**]
[**]Toward a Materialistic Foundation of Logic[*]
In this paper we shall make an attempt to develop a materialistic standpoint in the philosophical foundation of logic, directed against Empiricism, Conventionalism, and Rationalism, on the one hand, and against Nominalism and Platonism, on the other. Our analysis, starting from a conception of logic implicitly present or explicitly accepted by the majority of logicians [1] will be developed in three steps, including (a) quasi‑ontological presuppositions or prelogical (in case the term "ontology" would evoke misleading associations to some), (b) semantical assumptions and (c) an analysis of the concept of "existence."
The basic ideas of Materialism relevant for our purpose, especially the assertion of the priority of objective reality, are further developed in this specialized domain by adopting a "methodological materialistic dualism", consisting in the acceptance not only of a real world, but also of a world of ideas, the latter being the result of the practical and theoretical activities of mankind. This explicit extension seems necessary to us if the specific status of logic is to be adequately characterized, and if the usual claims of different idealistic interpretations of logic (which still prevail) are to be challenged. Some misunderstandings which might perhaps arise in this respect are due mainly to the traditional gap between logic, historically closely connected with Rationalism, and materialistic philosophy, focused primarily on the problems of the natural and social sciences.
On the philosophical level, the principal task of any satisfactory foundation of logic consists in an analysis of the relation of logic to experience and reality. What has always been conceived as an alleged paradox when dealing with logic, especially by empirically minded men, has been the contrast between the grounding of empirical knowledge by experience and the grounding of logic by itself. The logically valid propositional forms are valid simply by their form, without having to be tested by human experience. Why is deductive logic certain, whereas all other branches of science (with the exception of pure mathematics) yield no more than probable results? To this question several answers have been given.
From the philosophical standpoint of Empiricism, considered broadly, logical knowledge is nothing but a result of induction, and it differs from other kinds only by its more abstract nature. For Conventionalism, often combined with Subjective Idealism, the validity of logic is determined by linguistic conventions. From the standpoint of Rationalism, which is adopted in principle by Objective Idealists, the necessity of logic is given a priori or simply postulated (or it is felt to be an expression of the human mind's creativity).
All these explanations are undoubtedly one-sided. It must be maintained against Conventionalism, which played an important role in the philosophical conceptions of the Vienna Circle. that the L‑constants (being the basis of the definition of L‑following and hence also the fundament of logical proof, deducibility, or derivability of logical syntax) are not selected arbitrarily as linguistic conventions. We cannot presume that logic is wholly independent of experience and reality. It has an empirical basis, but not in the sense assumed by empiricists. All branches of science are primarily rooted in reality. Scientific activities and the results of science are at the very beginning conditioned by the reality reflected in our experience. From this obvious fact, which is sometimes briefly characterized by the dictum "nature is prior to man", it does not follow that in this simple form the genetic materialistic monism is eo ipso fully adequate as an explanation of the peculiarities of logic. To maintain such an attitude would mean that in any possible case only experience is relevant to science, and that theory plays but an advisory part, or that everything must be ultimately checked by experience. In connection with the manifold activities of man as zoon politicon, backed by the evolution of his linguistic habits, his capacities of theorizing have grown in such a manner that the formerly dependence of all his activities on reality has lost its compulsory character in certain domains. At a certain period of human history, a special. relatively independent "world of ideas" has emerged. The acceptance of this “reality" does not imply any Platonic world of ideas. The real world is one. Methodologically however, these two ''worlds", the real world and the "world of ideas", are fixed by language; these two are indispensable for any reasonable explanation of the theoretical sciences. Thus we have the conception of a genetic materialistic monism, reflecting the priority of nature, supplemented by a methodological materialistic dualism which takes into account the creativity of human activities. The assumption of these two "worlds", which Empiricism ignores and its opponents misinterpret, is a necessary condition for any understanding of the origin, development, and special status of formal logic as a science.
Against Empiricism we must argue with emphasis that its conception of the process of abstraction is a faulty simplification, one which cannot explain the special nature of logical constants. The definition of L‑constants cannot be conceived as simple collections of our experiences gained by the observation of the linguistic habits of men. Logic as any other science adopts various, historically determined empirical concepts, but this process is not a passive transposition of experience into theory. Every theoretical concept with the exception of primitive terms must be defined within the framework of a science. Any theory is thus connected with the formation of new concepts, relativized to the conceptual network of the theory in question. In logic, a formal science, the difference between empirical and theoretical concepts is evidently stronger than in any other factual science. This might be understood without any further specification as a clear expression of Conventionalism or Objective Idealism. If we stress only the creativity of conceptformation and disregard its empirical basis, we adopt this standpoint, ultimately yielding the conclusion that logical constants are no more than useful conventions.
As in any other theoretical science, concept‑formation in logic has more or less the character of idealization, which is (as commonly agreed) an indispensable tool of theory construction. Only if we misinterpret the process of idealization, which in different sciences admits different gradations, could one argue that we are defending a concealed conventionalistic standpoint. If we admit, however, idealization only in connection with its empirical basis, we reflect the actual practice of science. The relation of idealized concepts to empirical ones may not be factually traceable in every concrete case. It is only necessary to admit this possibility, because otherwise it would be impossible to explain the applicability of logic in both pure and applied science.
After this critical account of Empiricism and Conventionalism as the extremes of possible philosophic attitudes to logic, we may approach the more important questions which lead to the core of our inquiry. If we take into account the historical development of logic, its present systemization and its philosophical basis, it becomes clear that this relation must be understood in two senses, i.e., as an immediate and as a mediated relation. The available historical material shows clearly that the beginnings of logic are connected chiefly with the evolution of science and with an analysis of linguistic problems. The reflection of factual relations in reality is mediated through linguistically fixed thoughts. The analysis and codification of different kinds of reasoning, depending on propositions materially related to manifold facts, cannot but take into account the formal aspects. The relation of logic to reality is mediated through language. This fact, already manifest in the Stoic and Medieval logics, is a special, characteristic feature of modern logic. We can, of course, speak of an immediate relation of logic to reality if we ask what corresponds to logical constants in reality. This immediate relation is historically secondary, it does not characterize the trends of the evolution of logic. Yet if we attempt to find a satisfactory grounding of logic, it plays an important role.
From the very beginning, an analysis of the immediate relation of logic to reality in modern theoretical discussions was connected with the renewal of the problem of universals in logic and mathematics. [2] Modern controversies between Platonism and Nominalism deal with different problems, e.g., the problems of the existence of logical and mathematical entities, infinity, etc. With regard to our problem we are interested only in the question of ontological commitments concerning the relation of logic to reality and its theoretical reflection. [3] These questions are accepted by most logicians as reasonable, even if they are answered in a "neutral manner", as by R. Carnap. [4] They are contained for the first time in Aristotle's conception of logic. In latter developments of logic formerly firm connections between logic and the science of being were successively untied in favor of the connection of logic with language. From this historically and systematically conditioned divorce of logic from ontology (regretted in vain by the adherents of traditional logic and philosophy), it does not follow that logic is independent of ontology, in the sense that it has no relation to reality. That logic has no relation to reality was held not only by the Vienna Circle as an expression of their "antimetaphysical" attitude), but also by working logicians, especially in the purely syntactic period of modern logic. After the well‑known results of K. Godel, which destroyed all hopes of realizing Hilbert's programme, and of A. Tarski in the field of semantics; it was felt that logic cannot disregard the old philosophical controversies, but must handle them in a new way.
The necessity of establishing the range of admissible variables not only syntactically, but also semantically, led this time to considerations concerned with a categorization of their values. The categorization of entities designated or denoted by the variables of the language used in logic or mathematics was in a certain sense already established by Russell's theory of types. This syntactically oriented theory was at first introduced only ad hoc, in order to eliminate the logical paradoxes which arose in set theory and modern logic. With the semantical interpretation of the theory of types, it became clear that the hierarchy of entities established by it is in fact a quite natural categorization of designations which could or rather had to be introduced even though this had not been the original intension of B. Russell. The theory of types, in a certain sense anticipated by Aristotle's doctrine of categories, was therefore the first attempt to give a systematic basis for the language of logic. Now, if we take a further step and raise the question why the theory of types is adequate to the present purposes of logic, we evidently require a philosophical claim. This holds also for a semantical reinterpretation of the theory, as was attempted by Lesniewski.
In this situation, the older controversies in the philosophy of logic were replaced by the controversy between Platonism and Nominalism. Both participants in this controversy, in spite of irreconcilable standpoints, agree that a categorization of the entities designated or denoted by variables is a necessary assumption for any foundation of logic. The Nominalism in logic and mathematics represented by N. Goodman, W. V. Quine, and R. N. Martin, renounces abstract entities—classes, relations, properties, etc. The Platonism, represented by A. Church and H. Scholz admits all kinds of abstract entities, and in its extreme form considers them like Platonic Ideas. The dispute between Nominalism and Platonism with regard to the so‑called ontological problem is nowadays discussed on the basis of Quine's formulation of ontological commitments. According to this criterion, which was in principle admitted also by A. Church, [5] it depends on "the value of the variables and not on the supposed designata of the constant terms that the ontology of a theory is to be sought.” [6]
A language which admits variables that imply abstract entities as their values, e.g. classes, relations, etc., is considered as Platonistic; whereas a language which does not admit such variables is considered as nominalistic. As existentially quantifiable free variables such a language admits only individual variables. In the use of variables the Platonistic languages are unrestricted, provided that the theory of types is strictly adhered to.
If we accept this dichotomy and terminology the usual languages of logic and mathematics are Platonistic languages. The nominalistic philosopher of logic, who rejects the existence of abstract entities for philosophical reasons, is now facing a very difficult task if he wants to convince in a concrete fashion his philosophical opponents (or his neutrally minded colleagues among working logicians and mathematicians). He must prove that a nominalistic language can serve equally well all the needs of logic and mathematics. He therefore attempts a nominalistic reinterpretation of these languages. Since according to the criterion of ontological commitments in a nominalistic language only individual variables may have a designative function, he must try to reinterpret all predicates as syncategorematic terms, i.e., as expressions that have no independent meaning, and to reduce all proper names and definite descriptions to propositional forms with quantified individual variables.
We must here disclaim a deeper analysis of the absurd consequences of this reductionism and shall mention but two features of this project, the failure of which had to be admitted by Goodman and Quine themselves. We think that Nominalism fails to discern sufficiently sharply semantical and ontological decisions. From the reinterpretation of the language, no conclusions can be drawn in regard to an attempted philosophical foundation of a science. An elimination of certain linguistic expressions does not eliminate the denoted or designated entities.
Secondly, the argument of nominalists to the effect that, a philosophical problem can be solved on the level of language by semantic means, has most undesirable consequences. If we accept the dichotomy between nominalistic and Platonistic languages,, it follows that, because the nominalistic reinterpretation of Platonistic language failed (every scientific language with the languages of logic or mathematics as its framework must be a Platonistic language), every scientist is consciously or unconsciously bound to be a Platonist. We take for granted, however, that whether somebody declares himself a Platonist or nominalist, depends on personal philosophical beliefs, and not on the language he uses. From a language (its syntax and semantics) one cannot draw convincing conclusions about ontological questions. Ontological decisions, whether explicitly or implicitly formulated, are prior to semantical decisions and are a necessary part of the philosophical foundations of any science.
The result of this criticism is that we refuse to accept the dichotomy "Nominalism‑Platonism," considering that it leads to the conclusion that we must accept the Platonic solution. For an empiricist or materialist, Platonism as a philosophical conception, whether in its extreme or moderate form, is unacceptable.
It seems to us possible to find an appropriate philosophical foundation for logic that overcomes the horns of the dilemma., "Nominalism‑Platonism," and equally avoids redundant philosophical presuppositions which could stir up emotional feelings unacceptable for scientists with different philosophical beliefs. The suggested conception will admit only minimal philosophical assumptions.
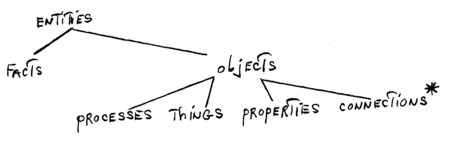
The philosophical foundations of logic will be found in a substantiated classification of semantical (and hence of syntactical) categories of the language of the formal sciences, based on a categorization of corresponding entities. This categorization will be called quasi‑ontology or prelogic, in order to show its similarity and dissimilarity to traditional ontology. We develop this quasi‑ontology on two levels. The quasi‑ontology of the first level can be summarized by diagram 1:
 [**]
[**]
The quasi‑ontology of the first level is based on the priority of reality, as well as on the assumption of the relative independence of the first member of the object‑subject relation in the theory of knowledge.
It assumes as real, i.e., existing in time and space, the following entities: facts, processes, things, properties and connections. Being interested only in the categorization of entities, we do not pay attention to the problem of an actual distinction of them. For our purpose it is thus irrelevant to ask, e.g. "What makes a thing a thing?"
Our categorization of objects is in fact broader than is needed in contemporary logic. Since it is possible to admit not only things but also processes, we can speak of two different quasi‑ontologies of the first level—a discrete and continuous one. Contemporary logic is based on a discrete quasi‑ontology. The question whether it would be possible to develop, on the basis of a continuous quasi‑ontology, another form of logic. e.g., a logic of processes, of actions, is quite reasonable and one can find at present several serious attempts in this direction.
The quasi‑ontology of the second level can be characterized by diagram 2:
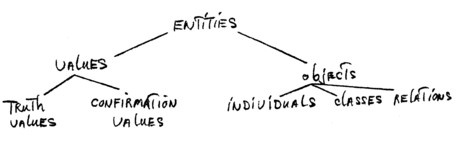
Whereas the entities of the quasi‑ontology of the first level are objectively given, those of the quasi‑ontology of the second level are postulated. These entities are idealized results of human activities. From a comparison of these two diagrams the following correspondences are manifest: Facts‑values, things-individuals, propertiesclasses, connections‑relations.
From these two quasi‑ontologies it follows that the hierarchy of entities of the theory of types (which is basically unlimited) is admitted only for the quasi‑ontology of the second level. The logic dealing with idealized entities is immediately related to the entities of the quasi‑ontology of the second level. But as these entities (being ideal constructions) are not constructed independently of entities of the quasi‑ontology of the first level, logic stands in a mediated relationship to reality. Our quasi‑ontologies are at the same time an expression of methodological materialistic dualism by assuming two worlds—the real world and the world of ideas.
From both categorizations, which show clearly the dependence of the quasi‑ontology of the second level on the quasi‑ontology of the first level, there follows as well our stand on the controversy between Platonism and Nominalism. The acceptance of the quasi‑ontology of the first level implies immediately a rejection of Nominalism by accepting not only a "world of individuals" in the sense of N. Goodman, but also a world with properties and connections. Platonism is stronger. We cannot reject it on the basis of our quasi‑ontologies. This becomes possible only if we develop a modified conception of semantics based on our quasi‑ontologies, and examine the problem of existence in logic.
Logical semantics in modern logic was founded by G. Frege's [7] conception, characterized by his well‑known distinction of Sinn and Bedeutung. G. Frege has developed what might be called a two‑dimensional semantics: a name expresses (druckt aus) its sense (Sinn) and denotes or means (bezeichnet, bedeutet) its meaning (Bedeutung). In this two-dimensional semantics, as I shall argue, two basically different semantical functions are identified, namely the function of bezeichnen and bedeuten. In respect to the special function of classical (two‑valued extensional) logic, this identification seems quite appropriate. For our purposes, especially if we are interested in the problem of the relation of logic to reality and try to avoid a Platonic solution (explicitly involved in Frege's conception), a revision of this two‑dimensional semantics is necessary. We shall propose a three-dimensional semantics, which presupposes the quasi‑ontologies of both levels. [8]
This three‑dimensional semantics which accepts as primary semantical categories the categories of "name" and "proposition," can be in either case characterized by diagram 3:
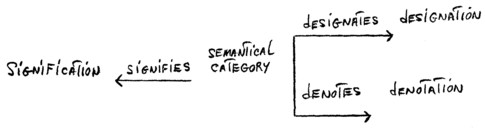
with three semantical functions: the signification‑, designation‑, and denotation‑function. The aim of this revision lies in the differentiation of the designation and denotation‑function in respect to our quasi‑ontologies: the designation‑function is related to the quasi‑ontology of the first level, and the denotation-function to the quasi‑ontology of the second level. This becomes manifest from a concretization of the above‑mentioned diagram:
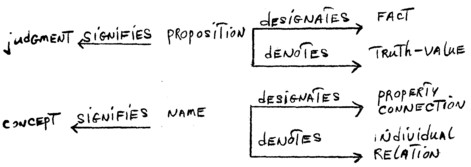
This refined distinction makes clear the real process of abstraction, combined with idealizations and constructions, a systematic classification of variables in respect to corresponding ranges of values. The range of values of variables is primarily determined by the designations and secondarily by the denotations. It would be advisable to change the usual terminology and speak either of variables in regard to the designations or denotations, but this would be too pedantic. [***] What is more important is an elucidation of the abstract step from fact to truth‑values, without accepting the Platonistic interpretation of truth‑values as abstract entities. It also becomes evident that logic cannot work with fact‑variables and is therefore compelled to substitute denotations, i.e., values, for the designations or propositions. It is true that in the case of names this substitution is not necessary, but this does not in principle weaken the conception that logic is only mediately connected with the quasi‑ontology of the first level.
The third step in the proposed philosophical foundation of logic (the problem of existence) deserves a somewhat broader introduction. It may, however, suffice to point out some fundamental remarks. This controversial problem, philosophically influenced by the refutation of the traditional existence‑proofs of God, has been studied, first of all in respect to its formal expression, as reflected by the introduction of the existential quantifier, and by the interpretation of propositions involving existence in such a manner that the very structure of these propositions clearly shows that existence is not a predicate. This can also be found in natural languages, especially in English, when we compare, e.g., the following pair of expressions "There are negative numbers" and "Negative numbers are". The interest of logicians and philosophers has further concentrated on questions involving different kinds of existence, and on the explanation of the concept of existence in connection with a distinction between what exists and does not exist, and how something exists or does not. These subject‑matters became urgent especially in mathematics, where the available means of exhibiting the entities which are asserted as existent are evidently different from other sciences. e.g., in zoology.
These questions were systematically analyzed for the first time by G. Frege and B. Russell, who being the chief advocates of Logicism, identified mathematical and logical existence. Because their logical systems were constructed with the intention to serve only the needs of mathematics, the concept of logical existence became a paradigm for all other kinds. In another regard this solution was strengthened by the Formalism of D. Hilbert, who explicitly and with consistency identified logical and mathematical existence. Against this simplification of mathematical existence was directed the criticism of the intuitionists, who refused to accept the admissibility of the existential import of propositions referring to infinite domains. The intuitionists suggest another interpretation based on the identification of mathematical existence with construction or constructibility. The controversy whether to accept the identification of mathematical existence with consistency or constructibility has not yet been decided in favor of the one or the other opposing conception. The claims of logicists and formalists cannot be considered as adequate. because they imply an identification of two domains—namely logic and mathematics—which are methodologically very near, but substantially different. Neither can the claims of intuitionists be accepted, considering that (in so far as classical mathematics is concerned) they imply the existence only of entities of finite domains. The requirement of actual constructions, which is the core of their intention, cannot be realized for the objects of infinite domains. If we agree that mathematical entities are entities gained by idealization, construction, and abstraction; we must nevertheless differentiate whether we are concerned with entities of finite or infinite domains. For finite domains an actual exhibition is possible, but for infinite domains it is not possible.
For the present purpose the special aspects of mathematical existence are less important, and it may suffice to say that for the existence of different mathematical entities we would like to propose different explications; actual constructions, i.e., constructions in a stronger sense, or finite entities a construction in a weaker sense, including the axiomatic method and the theory of models of infinite entities. This liberal attitude expresses our conviction that, for the entities of a certain science, we cannot formulate but one criterion of existence.
What seems to be more important is, first of all, a clear differentiation between logical existence (L‑existence) on one hand and different kinds of factual existence (Fexistence) on the other, or between logical, ideal and factual existence. L‑existence can be in fact identified with consistency. For logic all entities exist which are subjected to the principium contradictionis. In this sense logic, or more explicitly classical elementary logic, can be applied in all "possible worlds" (in the sense of Leibniz), or, as we would say nowadays, in all the domains of individuals. These domains are in principle non‑empty, because the assumption of logical existence rules out all internally inconsistent entities. From the standpoint of L-existence only the impossible world is empty, and cannot therefore contain any entities.
Besides L‑existence we can distinguish different kinds of F-existence (in a broad sense), if we want to underline the difference between consistency and special criteria of existence in all other cases than in the case of L‑existence. However, another refined classification of non‑logical or F‑existence is also possible. First of all, we can speak of F‑existence (in a narrow sense) and ideal existence, including (as the most distinguished case) mathematical existence. Secondly, we can further subclassify in accordance with different strata of reality.
From this standpoint we cannot consider as convincing the famous argument about the non‑existence of Pegasus, centaurs, and so on. When we speak of the alleged nonexistence, then we have in mind entities of domains described by zoology, or entities having some kind of Fexistence. If we have in mind another context, namely the framework of Greek mythology, i.e., some kind of ideal existence, we cannot deny that they are nonexistent. Without reference to a definite domain of entities, there is no point in speaking about existence or non‑existence. This relativization does not only hold in such extreme, often artificially selected, cases, but also in regard to entities which are commonly accepted as existent. To speak about the existence of a neutron in the system of classical physics is to speak about a non‑existent entity. This attempted classification of existence, methodologically related to a conception or relative existence, stands in clear opposition to all concepts of existence absolutely conceived by metaphysicians.
In practice the relativization of existence is connected with different criteria for establishing whether something exists or does not. As is already known, for L‑existence we have assumed consistency, for physical existence one can adopt subsistence in time and space. For these reasons all disputes about whether something exists or not are simply idle, when a corresponding framework is undetermined.
As presumably already recognized, this standpoint is partially influenced by Carnap's distinction of internal and external existential questions and statements. We are similarly interested only in the existence of entities relative to a fixed domain. This holds also in the case of our quasi‑ontologies. When the existence of facts and/or of truth values, of things, of individuals, etc., is assumed, only their relative existence in respect to these quasi‑ontologies as forming their framework is meant as well in regard to other entities of each of them. We do not postulate that there exist, e.g., things as such, but only assume that there are things, without being concerned with their special nature. It is, of course, quite clear that in reality there are only specific things, not things in general. The relativization of entities is determined also by their mutual relations: the existence of one entity influences the existence or non‑existence of another. We cannot speak of an existing thing without assuming that it has certain properties and is devoid of others. The acceptance of the suggested stratification of reality, reflected in the quasi‑ontology of the first level, being at the same time the basis of a further stratification related to those of the quasi‑ontology of the second level, has no intended metaphysical implications.
We neither make the attempt to reduce the proposed entities nor do we try to explain, e.g., what makes a thing a thing.
What conclusions can be drawn from the above-mentioned analysis of existence for the criticism of Nominalism and Platonism in logic? The existence of the entities of the quasi‑ontology of the first level must be evidently understood as factual (in a broad sense), relativized in respect to different subclassifications. The conception of the quasi‑ontology of the first level is, of course, an idealization, needed for our philosophical grounding of logic. The existence of the entities of the quasi‑ontology of the second level can be characterized as ideal existence. Truth‑values, individuals, classes, and so on, are idealized entities and their existence is clearly distinct from the entities of the quasi‑ontology of the first level.
The question whether there are, e.g., classes or not, if formulated in this way, is inexact, and cannot therefore be unambiguously answered. We can only ask whether they are or are not factual or ideal. In the former case our answer will be negative, in the later case positive. Because ideal existence is without any doubt different from the factual, we cannot assign to the entities of the quasi‑ontology of the second level temporal and spatial coordinates. The often raised question "And how do ideal entities exist?", with the implicit allusion to the answer, "They exist in our minds" is only an expression of an anthropomorphic analogy with the existence of physical entities in time and space. To interpret entities with ideal existence as independent objects sui generis is tantamount to misinterpreting their genesis, which is historically and systematically based on the entities of the quasi‑ontology of the first level. To consider them in the traditional sense of Platonism as entities in a realm of Ideas is doubtless an unfounded metaphysical supposition. This extreme standpoint finds, of course, its support in Nominalism by its one‑sided (in principle empiricistic) conception, admitting only one kind of existence, i.e., factual or physical existence. The unacceptable consequences of both conceptions—that of Platonism and that of Nominalism—can in our opinion be avoided by our differentiation and relativization of existence in respect to different frameworks.
By this exposition of the nature of existence in the framework of our proposed materialistic foundation of logic, we are concluding this paper, without pretending to have exhausted this controversial subject‑matter.
Czechoslovak Academy of Sciences
The Institute for Theory and Methododology of Science
Notes
* Reprinted by permission of the author. Dr. Berka's article originally appeared in the Czech journal Teorie a Metoda, 1969. Article abridged for inclusion in this volume. [—> main text]
** Used for terminological reasons in order to differentiate as in German between "Beziehung" and "Relation," or as in Czech, between "vztah" and ''relace.'' See our paper "Logik und 'Ontologie': Kritische Bemerkung zum zeitgengössischen Universalienstreit," DZfPh 7/1967. [—> main text]
*** A reclassification of variables could serve in any case for a distinction of different kinds of logical languages, a terminological precization and an elucidation of the concept of extension and intension in logic. [—> main text]
1. A discussion of this conception is, e.g., contained in our paper "Über den Gegenstand der formalen Logik", DZfPh 12/6 (1964), pp. 1102‑1111. [—> main text]
2. Cf. e.g., W. Stegmüller, "Das Universalienproblem, einst und jetzt", in Archiv für Philosophie, 6 (1956) pp. 192‑225, 7 (1957) pp. 45‑81; G. Küng, Ontologie und logische Analyse der Sprache. Eine Untertsuchung zur zeitgenössischen Universaliendiskussion, Wien, 1963. [—> main text]
3. Cf., e.g., W. V. Quine, From a Logical Point of View. Nine Logico‑Philosophical Essays, Cambridge, Mass., 1953; L. Tondl, Problémy sémantiky, Praha, 1966, pp. 302ff. [—> main text]
4. See "Empiricism, Semantics, and Ontology," in Revue Inter. de Phil., 4 (1950), pp. 20‑40. [—> main text]
5. "Ontological Commitments," The Journal of Philosophy, LV (1958) p. 1013. [—> main text]
6. N. Goodman & W. V. Quine, "Steps Toward a Constructive Nominalism," JSL 12, 1947, p. 105, note 1. [—> main text]
7. "Über Sinn und Bedeutung"" Z. F Phil. u. Phil. Kritik, 100 (1892), pp. 25‑50. [—> main text]
8. See also K. Berka & L. Kreiger, "Eine grundsätzliche Erweiterung der Semantik G. Freges," DZfPh 10/1968. [—> main text]
SOURCE: Berka, Karel. "Toward a Materialistic Foundation of Logic," in: Contemporary East European Philosophy, vol. 3, edited by Edward D'Angelo, David H. DeGrood, Dale Riepe (Bridgeport, CT: Spartacus Books, 1971), pp. 182-204.
Additional references:
Berka, Karel. “Existence in Modern Logic,” in Essays in Metaphysics, by members of the Philosophy Dept., Pennsylvania State University, edited by Carl G. Vaught (University Park: Pennsylvania State University Press, 1970), pp. 157-174.
__________. Measurement: Its Concepts, Theories, and Problems [Měření], translated from the Czech by Augustin Riska. Dordrecht; Boston: D. Reidel Publishing Company, 1983. (Boston Studies in the Philosophy of Science; v. 72)
__________. “Rational and Nonrational Elements in the History of Science,” in Physics, Philosophy, and the Scientific Community: Essays in the Philosophy and History of the Natural Sciences and Mathematics in Honor of Robert S. Cohen, edited by Kostas Gavroglu, John Stachel, Marx W. Wartofsky (Dordrecht; Boston: Kluwer Academic, 1995), pp. 273-285. (Boston Studies in the Philosophy of Science; v. 163)
__________. “Scales of Measurement,” in Language, Logic, and Method, edited by Robert S. Cohen and Marx W. Wartofsky (Dordrecht; Boston: D. Reidel Publishing Company, 1983, pp. 1-73 (Boston Studies in the Philosophy of Science; v. 31)
“What
is the Relationship Between Logic and Reality?”
by R. Dumain
Salvaging Soviet Philosophy (1)
Offsite:
The Concept of Existence: Definitions by Philosophers
On the Czech Logic in the 20th Century
by Jiří Raclavský
Home Page | Site
Map | What's New | Coming Attractions | Book
News
Bibliography | Mini-Bibliographies | Study
Guides | Special Sections
My Writings | Other Authors' Texts | Philosophical
Quotations
Blogs | Images
& Sounds | External Links
CONTACT Ralph Dumain
Uploaded 20 May 2004
References & links added 5 September 2021
Site ©1999-2021 Ralph Dumain